Recent Projects

1. Macroscopic Dynamics for Nonequilibrium Chemical Reactions

Most biochemical reactions in living cells are an open system interacting with the environment through chemostats. At a mesoscopic scale, the molecular number of each species in those biochemical reactions can be modeled by the random time-changed Poisson processes.

To characterize the macroscopic behaviors in the large volume limit, the law of large numbers in path space determines a mean-field limit nonlinear ODE. At the same time, the WKB expansion yields a Hamilton-Jacobi equation and the corresponding Lagrangian gives the good rate function in the large deviation principle (LDP). The rigorous convergence of Varadhan’s discrete nonlinear semigroup (recast as a monotone scheme) to the continuous Lax-Oleinik semigroup yields the large deviation principle for the chemical reaction process at any single time. Consequently, the macroscopic mean-field limit reaction rate equation is recovered. Moreover, the LDP for invariant measures can be used to construct the global energy landscape for non-equilibrium reactions. This enables the dissipative-conservative decomposition for the Hamilton dynamics of chemical reactions, which also facilitates the understanding of thermodynamics.

The LDP for the invariant measure also provides a selection principle that selects a unique weak KAM solution to the corresponding stationary HJE. The weak KAM solutions for stationary Hamilton-Jacobi equations (HJE) is a key tool to study the long time behaviors of dynamical systems, such as the Mather measures or invariant sets. However, there are in general an infinite number of weak KAM solutions. The selected weak KAM solution has a variational principle with globally determined boundary values at the Aubry set and the Peierls barriers computed from the least action cost in an infinite time horizon starting from points in the Aubry set.

2-autocatalysis non-equilibrium chemical reaction
Borrow from M.C. Escher
Global energy landscape serves as a selected weak KAM solution
Decomposition and thermodynamics for
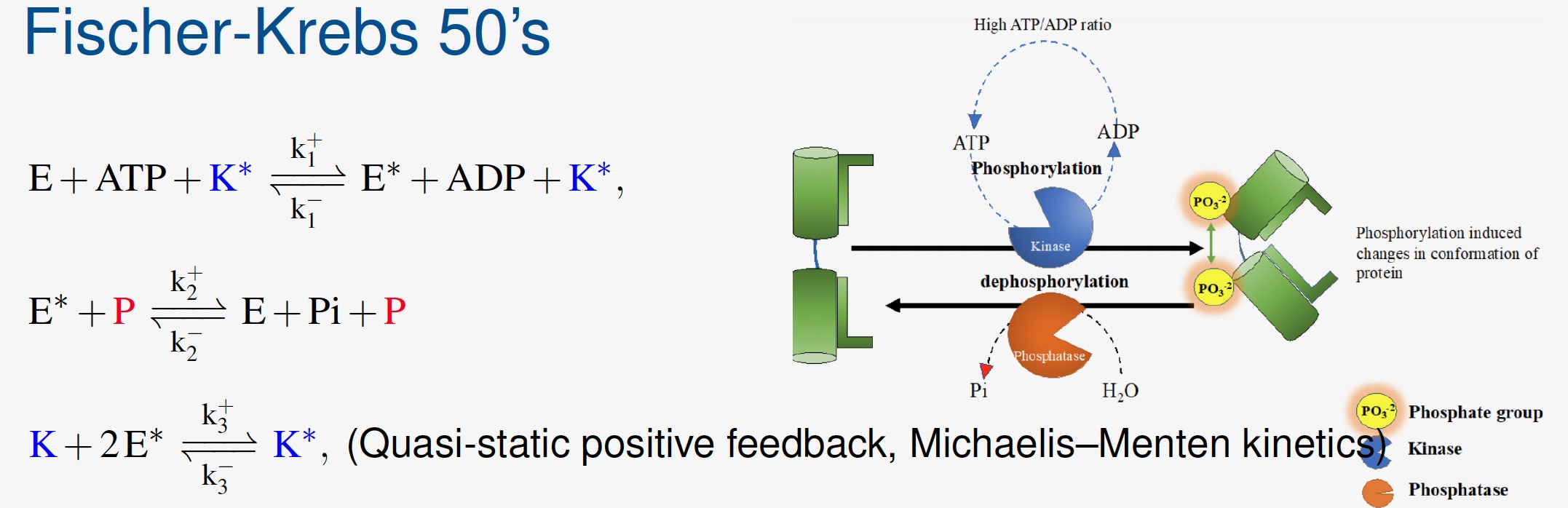
non-equilibrium chemical reaction with non-equilibrium stationary state (NESS)

Related publications:

  1. Gao, Y., and J. -G. Liu. Revisit of macroscopic dynamics for some non-equilibrium chemical reactions from a Hamiltonian viewpoint. Journal of Statistical Physics. 189(22). (2022). Full text:
  2. Gao, Y., and J. -G. Liu. Random walk approximation for irreversible drift-diffusion process on manifold: ergodicity, unconditional stability and convergence. Communications in Computational Physics. 34(1): 132-172. (2023). Full text:
  3. Gao, Y. and J. -G. Liu. Large deviation principle and thermodynamic limit of chemical master equation via nonlinear semigroup. Multiscale Modeling and Simulation. 21(4): 1534-1569. (2023). Full text:
  4. Gao, Y., and Y. F. Zhou. Hamilton Dynamics in Chemical Reactions: the Maupertuis Principle, Transition Paths and Energy Landscape. Communications in Mathematical Analysis and Applications, 2(3): 245-288. (2023). Full text:
  5. Gao, Y., and J. -G. Liu. A selection principle for weak KAM solutions via Freidlin-Wentzell large deviation principle of invariant measures. SIAM Journal on Mathematical Analysis, 55(6): 6457-6495. (2023). Full text:

2. Optimal control and mean field game for chemical reactions and particle systems

Optimal control for single particle and mean-field control for interacting particle system has broad applications across interdisciplinary fields such as biology, physics, materials science, data science, and social sciences. In these interactive dynamics, non-typical trajectories with large fluctuations occur with small probability but are fundamental events such as protein folding and species evolution/extinction. A fundamental question is to predict and control these non-typical behaviors in interactive dynamics on complex configuration spaces, such as transition paths between metastable states on chemical reaction networks.

We explore a stochastic optimal control formulation for transition path problems in an infinite time horizon, for both dynamics modeled by diffusion processes or Markov jump processes on Polish spaces. An unbounded terminal cost at a stopping time, along with a controlled transition rate, regulates the transitions between metastable states. The optimal control to proved to maintain the original bridges with the running cost suggested by the rate function in the large deviation principle. Girsanov transforms and Gamma-convergence techniques will be adapted to justify the singular optimal control. The optimally controlled process realizes the transition paths almost surely but without altering the bridges of the original process.

Mean field games and mean field control model the collective behaviors of interacting individual/particles, which can be regarded as the mean field limit of N-player games or N-particle system. The resulting optimal control problem is an optimization problem in a probability density space equipped with Wasserstein metrics. For a discrete configuration space, analogous Nash systems and master equations can be derived with variational principles. The associated continuity equation on a graph with a nonlinear activation function generalizes the usual discrete Wasserstein metrics. The variational principle can also be generalized to non-potential games given the information of Nash equilibriums. For a continuous configuration space, the homogenization of the Wasserstein distance and the Wasserstein gradient flow structure for the mean field limit PDE can be proved by evolutionary Gamma-convergence techniques and the variational principles. The exchange of mean field limit, the large time limit and the oscillation parameters in the homogenization limit is a challenging open question.

Optimal control formulation for rare events and transition paths between metastable sets
Mean-field control for complex fluid with different loss
Collective behaviors for large number of particles

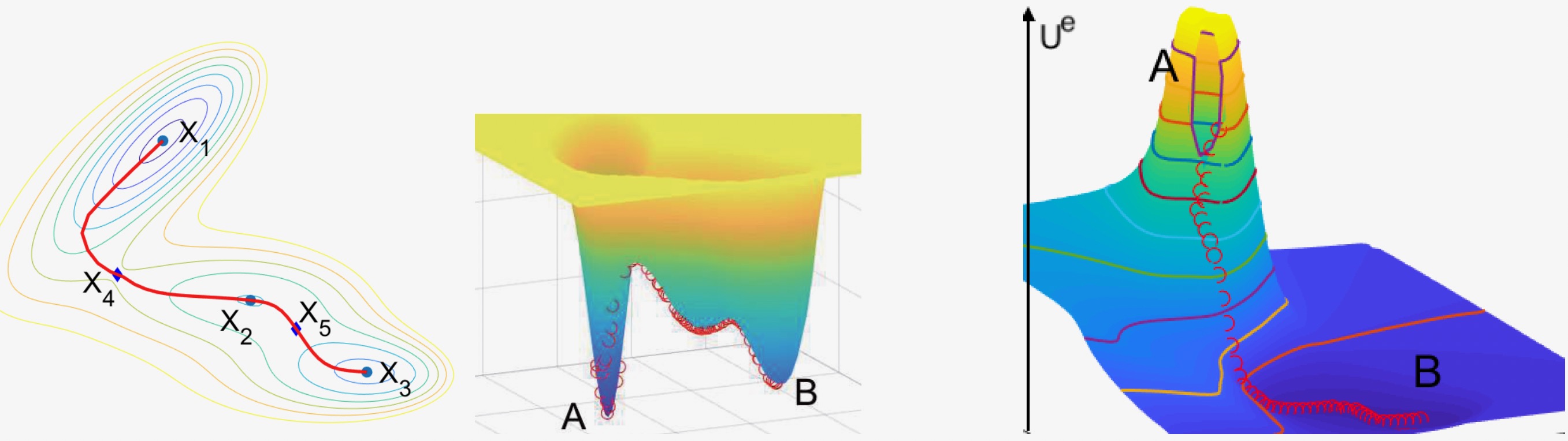
Related publications:

  1. Gao, Y., T. Li, X. Li, and J. -G. Liu. Transition path theory for Langevin dynamics on manifold: optimal control and data-driven solver. Multiscale Modeling and Simulation. 21(1): 1-33. (2023). Full text:
  2. Gao, Y., W. Li, and J. -G. Liu. Master equations for finite state mean field games with nonlinear activations. Discrete and Continuous Dynamical Systems Series B, 29(7): 2837-2879. (2024). Full text:
  3. Gao, Y., J. -G. Liu, O. Tse. Optimal control formulation of transition path problems for Markov Jump Processes. submitted.
  4. Gao, Y., W. Li, J. -G. Liu. Fluctuations in Wasserstein dynamics on Graphs. submitted.
  5. Gao, Y., N. K. Yip. Homogenization of Wasserstein gradient flows. submitted.
  6. Gao, Y., D. Qi. Mean Field Games for Controlling Coherent Structures in Nonlinear Fluid Systems. submitted.

3. Obstacle problem: moving contact lines, lubrication

The dynamics and equilibrium of a droplet on a substrate are important problems with many practical applications such as coating, painting in industries and the adhesion of vesicles in biotechnology. Particularly, the contact line dynamics of a droplet placed on an inclined rough surface are challenging fluid mechanics problems dated back to Young in 1805. The capillary effect, which contributes the leading behaviors of the geometric motion of a small droplet, is characterized by the surface tensions on interfaces separating two different physical phases.

The geometric dynamics of the droplets are described by the mean curvature flow of the capillary surface, coupled with the moving contact lines (where three phases meet), which contributes the leading driven force for the droplet dynamics. The dynamic contact angles tend to go to the equilibrium contact angle (Young’s angle) following the contact line speed mechanism proposed by de Gennes. We focus on the 2nd order unconditionally stable numerical schemes for simulating droplets dynamics on a inclined rough surface with topological changes, such that merging and splitting.

After lubrication approximation, we also investigated the resulting fluid thin film system. A spatial variation in a thin lipid layer leads to locally elevated evaporation rates of the tear film, which in turn affects the local salt concentration in the liquid film. After considering all the contributions from evaporation, capillarity and osmolarity, a general model can capture the key features of tear-film dynamics and rupture with power-law mobility functions.

Rupture in tear film dynamics with evaporation, capillarity and osmolarity
Kelvin pendant droplets with bulge or lightbulb shape
Splitting of droplet due to rough substrate
Merging of droplets and contact angle hysteresis

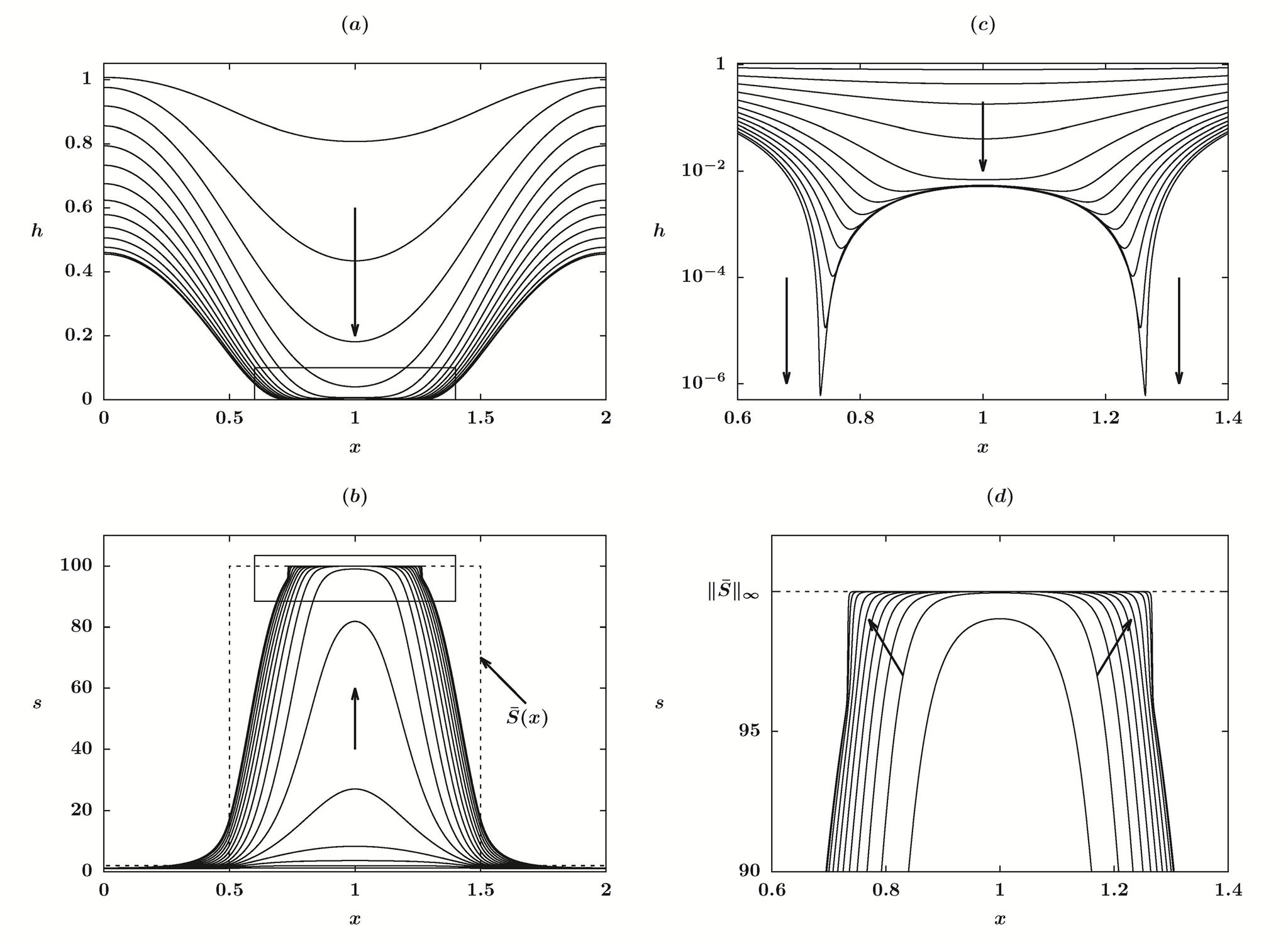
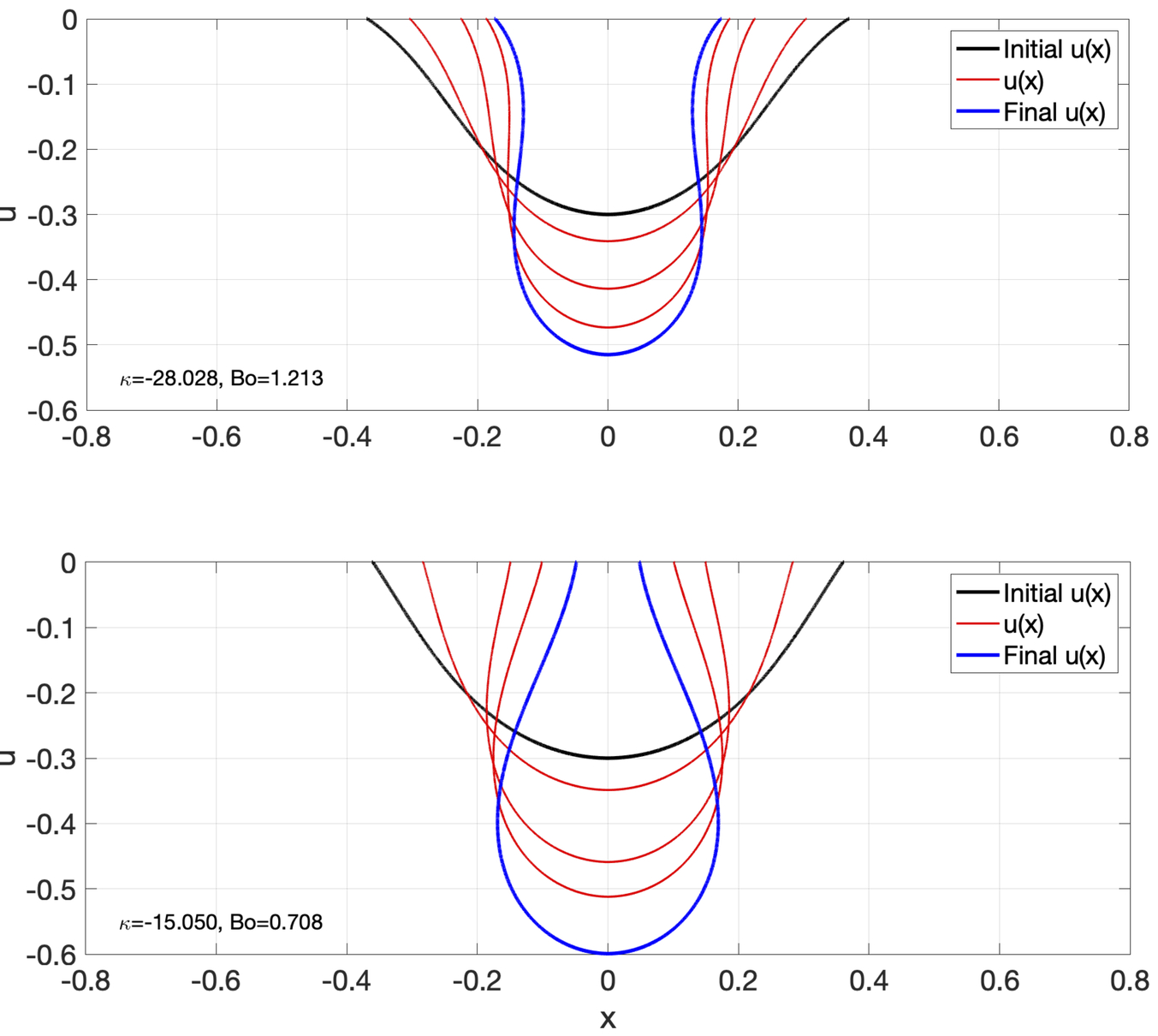
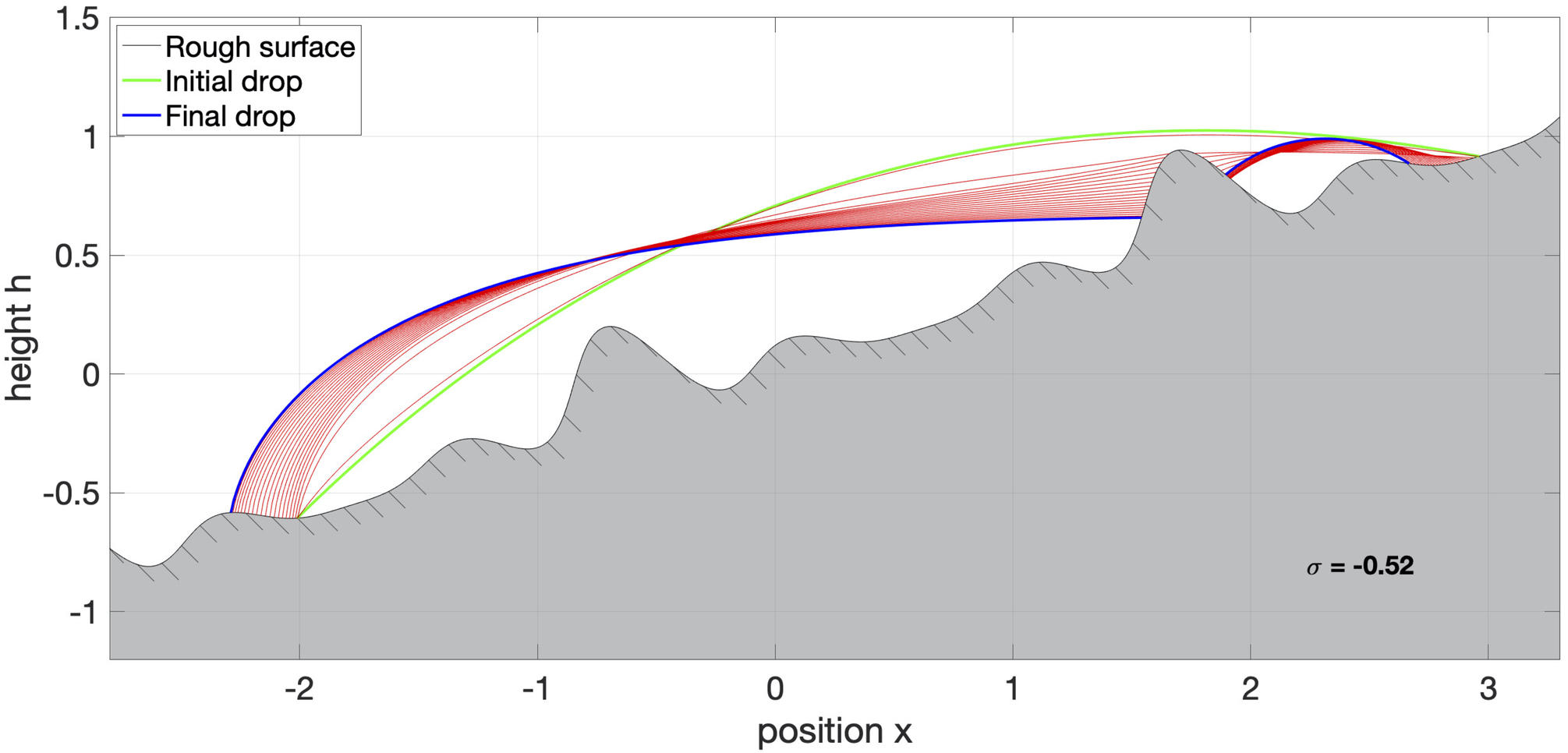
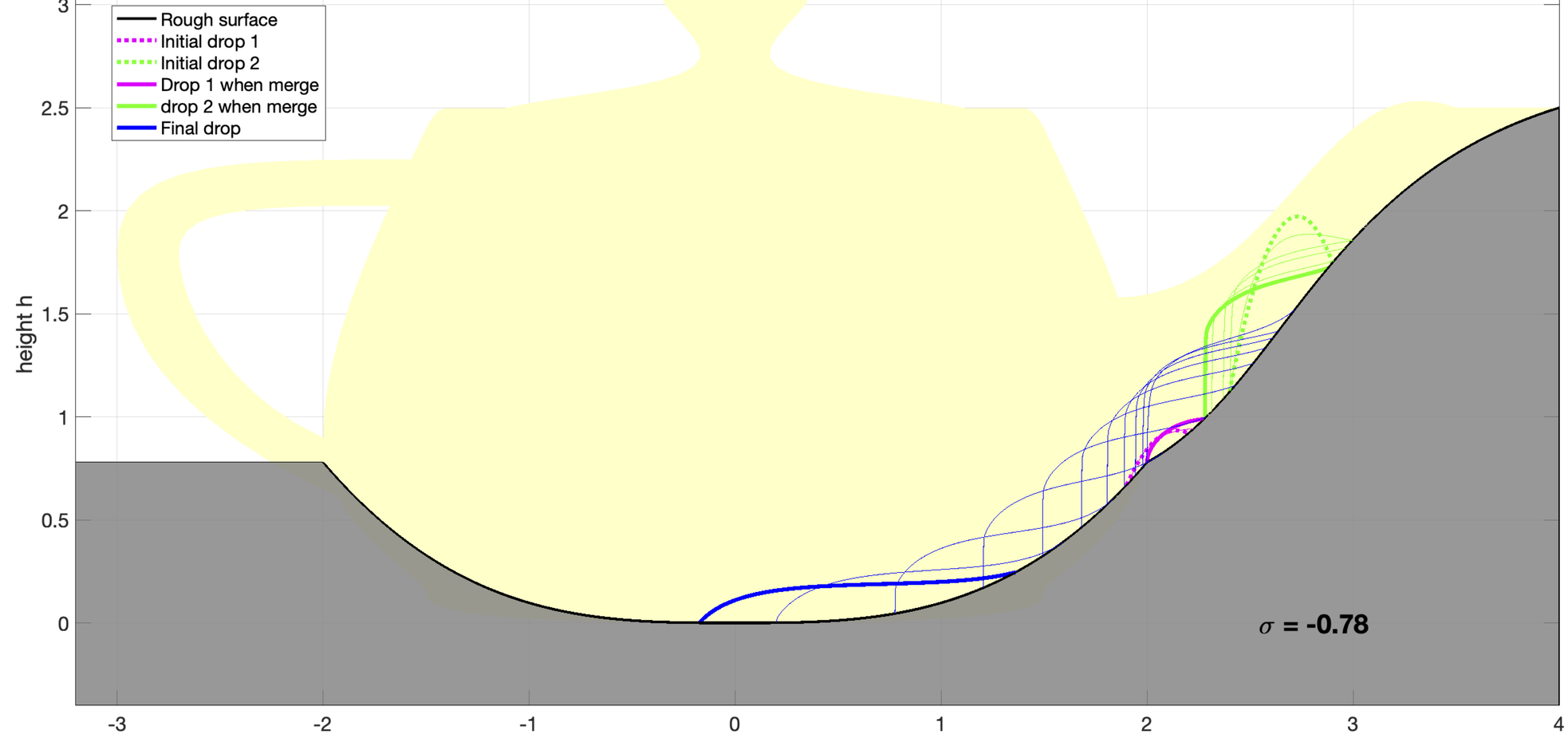
Related publications:

  1. Gao, Y., H. Ji, J.-G. Liu, and T. P. Witelski. Global existence of solutions to a tear film model with locally elevated evaporation rates. Physica D: Nonlinear Phenomena. 350: 13–25. (Jul 1, 2017). Full text:
  2. Gao, Y., and J.-G. Liu. Gradient flow formulation and second order numerical method for motion by mean curvature and contact line dynamics on rough surface. Interfaces and Free Boundaries. 23(1): 103–158. (Apr 19, 2021) Full text:
  3. Gao, Y., and J.-G. Liu. Surfactant-dependent contact line dynamics and droplet adhesion on textured substrates: derivations and computations, Physica D: Nonlinear Phenomena. 428: 133067. (Oct 12, 2021). Full text:
  4. Gao, Y., and J.-G. Liu. Projection method for droplet dynamics on groove-textured surface with merging and splitting, SIAM Journal on Scientific Computing. 44(2): B310–B338. (Mar 21, 2022). Full text:

4. Motion of materials defects: dislocations and grain boundaries

Dislocations are line defects in crystalline materials and they play essential roles in understanding materials properties like plastic deformation and in the development of novel materials with robust performance.

The detailed structure in a dislocation core can be described by the Peierls-Nabarro (PN) model, which is a multiscale continuum model that incorporates the atomistic effect by introducing a nonlinear potential describing the nonlinear atomistic interaction across the slip plane of the dislocation. We focus on existence, De Giorgi-type 1D symmetry, uniqueness and asymptotic stability of the original 3D vectorial dislocation model.

Related publications:

  1. Gao, Y., J.-G. Liu, T. Luo, and Y. Xiang. Revisit of the Peierls-Nabarro model for edge dislocations in Hilbert space. Discrete and Continuous Dynamical Systems Series B. 26(6): 3177-3207. (Jul 2020)
  2. Gao, Y., and J.-G. Liu. Long time behavior of dynamic solution to Peierls–Nabarro dislocation model. Methods and Applications of Analysis. 27(2): 161–198. (Jul 27, 2020) Full text:
  3. Dong, H., and Y. Gao. Existence and uniqueness of bounded stable solutions to the Peierls–Nabarro model for curved dislocations. Calculus of Variations and Partial Differential Equations. 60(2): 62. (Apr 3, 2021). Full text:
  4. Gao, Y., J.-G. Liu, and Z. Liu. Existence and rigidity of the Peierls-Nabarro model for dislocations in high dimensions, Nonlinearity. 34(11): 7778–7828. (Oct 6, 2021). Full text:
  5. Gao, Y. and J.-M. Roquejoffre. Asymptotic stability for diffusion with dynamic boundary reaction from Ginzburg-Landau energy. SIAM Mathematical Analysis. 55(2): 1246-1263. (2023) Full text:
  6. Gao, Y., and J.-M. Scott. Existence and uniqueness of solutions to the Peierls-Nabarro model in anisotropic media. Nonlinearity, 37: 1-30. (2024). Full text:

5. Langevin dynamics, rare events

Langevin dynamics with an energy landscape representing the stable or metastable states are often used to describe various physical system satisfying the fluctuation-dissipation relation. More importantly, irreversible drift-diffusion processes are very common in biochemical reactions and the irreversibility in circulation balance is indeed an primary characteristic of life activities. They have a non-equilibrium stationary state (invariant measure) which does not satisfy detailed balance.

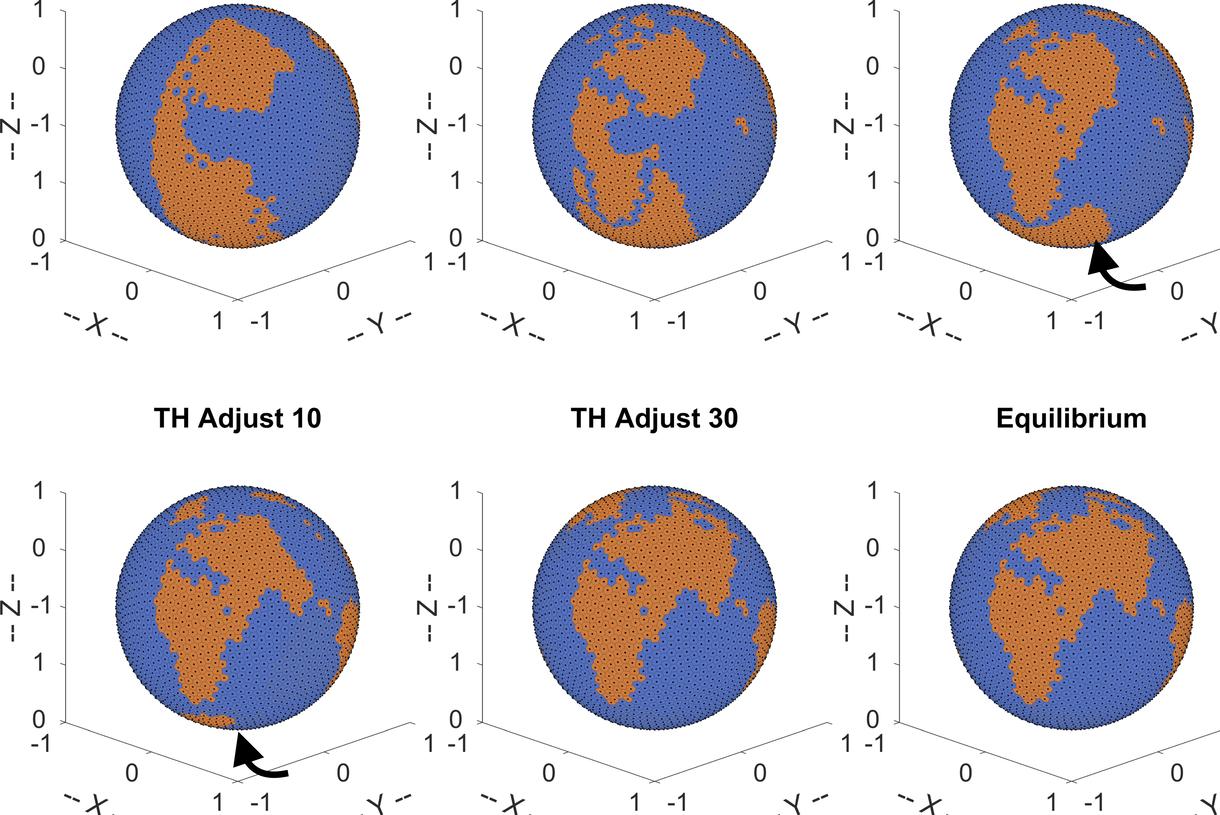
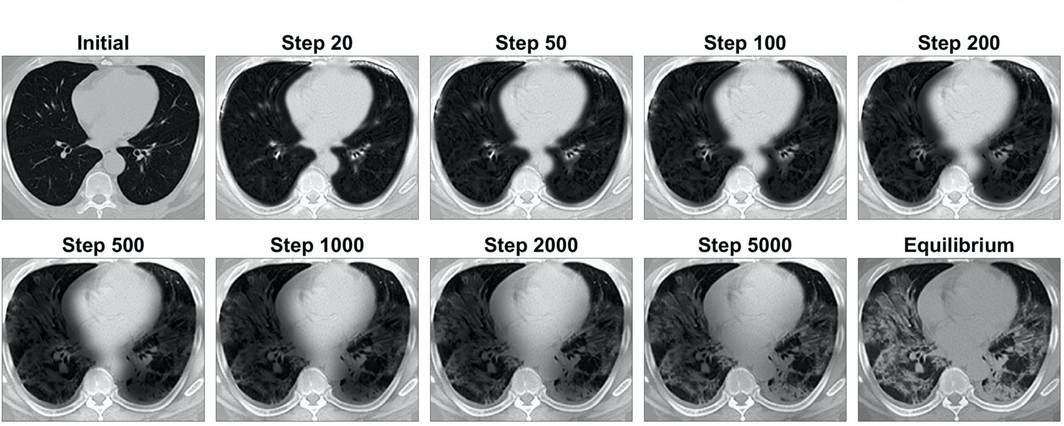
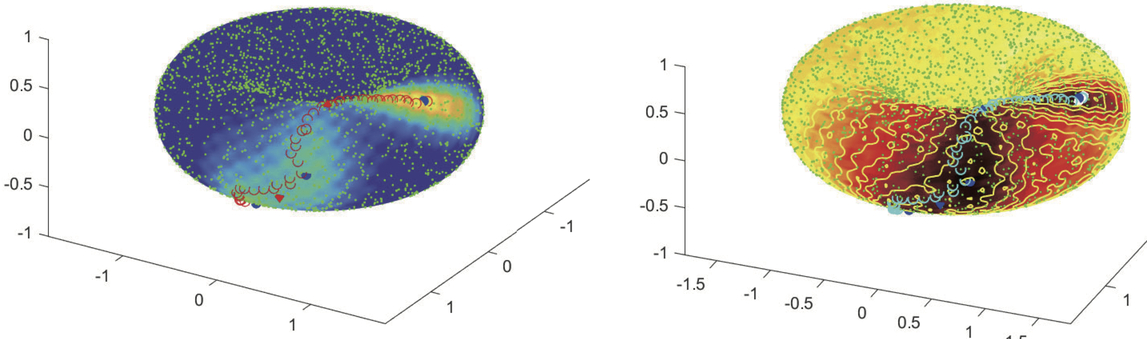
To simulate those Markov processes, designing structure-preserving numerical schemes which enjoys stochastic Q-matrix structure and symmetric decomposition are very important. Those algorithms assign the transition probability on point clouds and thus naturally give random walk approximations for a generic Markov process on a manifold. Thus combining with collected point clouds probing the manifold (induced from nonlinear dimension reduction such as diffusion map), those algorithms can be easily adapted to manifold-related computations such as finding the transition path in a rare event such as protein folding.

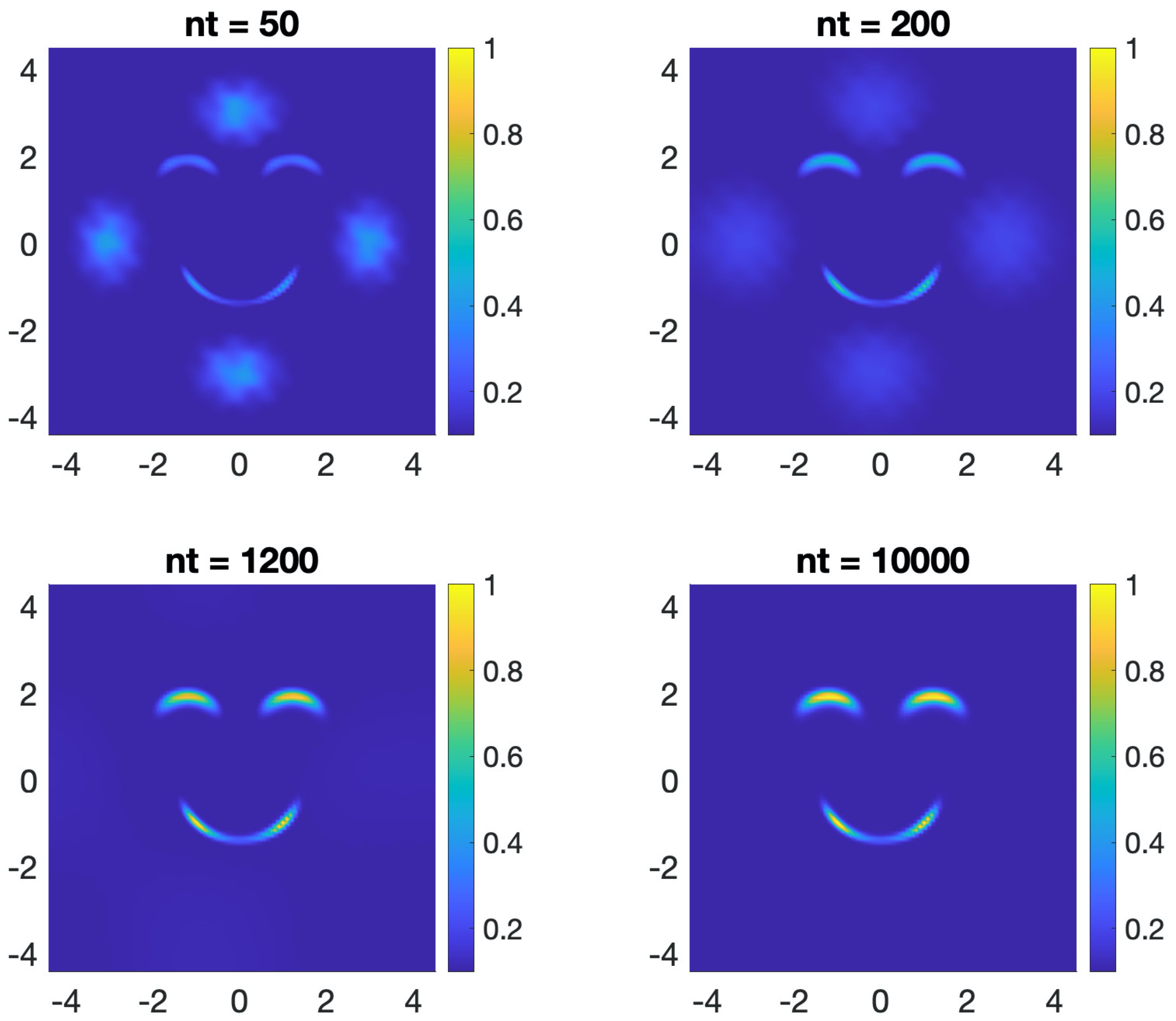
Various promising interdisciplinary applications are conducted including efficient sampling enhanced by a mixture flow, auto-inbetweening image transformation, optimal controlled Monte Carlo simulation for conformational transitions and simulations of shape dynamics on manifold.

Aging process of human faces
Continental drift process via data-driven simulation
Simulated pneumonia invading lungs caused by COVID-19 on CT images
Transition path simulation via optimally controlled random walk on point clouds
Accelerated sampling triple-banana via irreversible dynamics
Image transformation immersed in an incompressible mixture flow

Related publications:

  1. Gao, Y., G. Jin, and J.-G. Liu. Inbetweening auto-animation via Fokker-Planck dynamics and thresholding. Inverse Problems and Imaging. 15(5): 843-864. (Oct, 2021) Full text: Video for facial aging process:
  2. Gao, Y., T. Li, X. Li, and J.-G. Liu. Transition path theory for Langevin dynamics on manifold: optimal control and data-driven solver. Multiscale Modeling and Simulation. 21(1):1-33. (January, 2023) Full text:
  3. Gao, Y., J. -G. Liu, and N. Wu. Data-driven Efficient Solvers for Langevin Dynamics on Manifold in High Dimensions. Applied and Computational Harmonic Analysis. 62(2023):261-309. (January, 2023) Full text:
  4. Gao, Y., and J.-G. Liu. Random walk approximation for irreversible drift-diffusion process on manifold: ergodicity, unconditional stability and convergence. Communications in Computational Physics. 34(1): 132-172. (2023). Full text:
  5. Liu, C., Y. Gao, and X. X. Zhang. Structure preserving schemes for Fokker-Planck equations of irreversible processes. Journal of Scientific Computing, 98(4). (2024). Full text:

6. Crystal growth

Epitaxial growth is a process in which adatoms are deposited on a substrate and grow a solid thin film on the substrate. In general, PDEs modeling macroscopic dynamics in non-equilibrium dynamics are usually guided by the underlying competing mechanism at the microscopic level. Meanwhile, an effective description of the microscopic dynamics, using equilibrium Gibbs measure or non-equilibrium optimal twist measure, is suggested by macroscopic observations. We also derive the continuum limit PDE from the surface hopping process on lattice and give validations via kinetic Monte Carlo.

From a larger mesoscopic scale, Epitaxial growth is described by step flow dynamics driven by misfit elasticity between thin film and the substrate. The discrete Burton-Cabrera-Frank (BCF) type models have been proposed by Burton, Cabrera, Frank, Duport, Tersoff, et al.. From the macroscopic view, the governing equations for thin film growth processes are all high order degenerate parabolic equations. We focus on the analytic validation of those continuum models by studying the continuum limit from discrete model, global positive solution, strong solutions with latent singularities and long-time behavior of solutions. The facet formation for some nonlocal misfit elasticity with fat tails is still open.

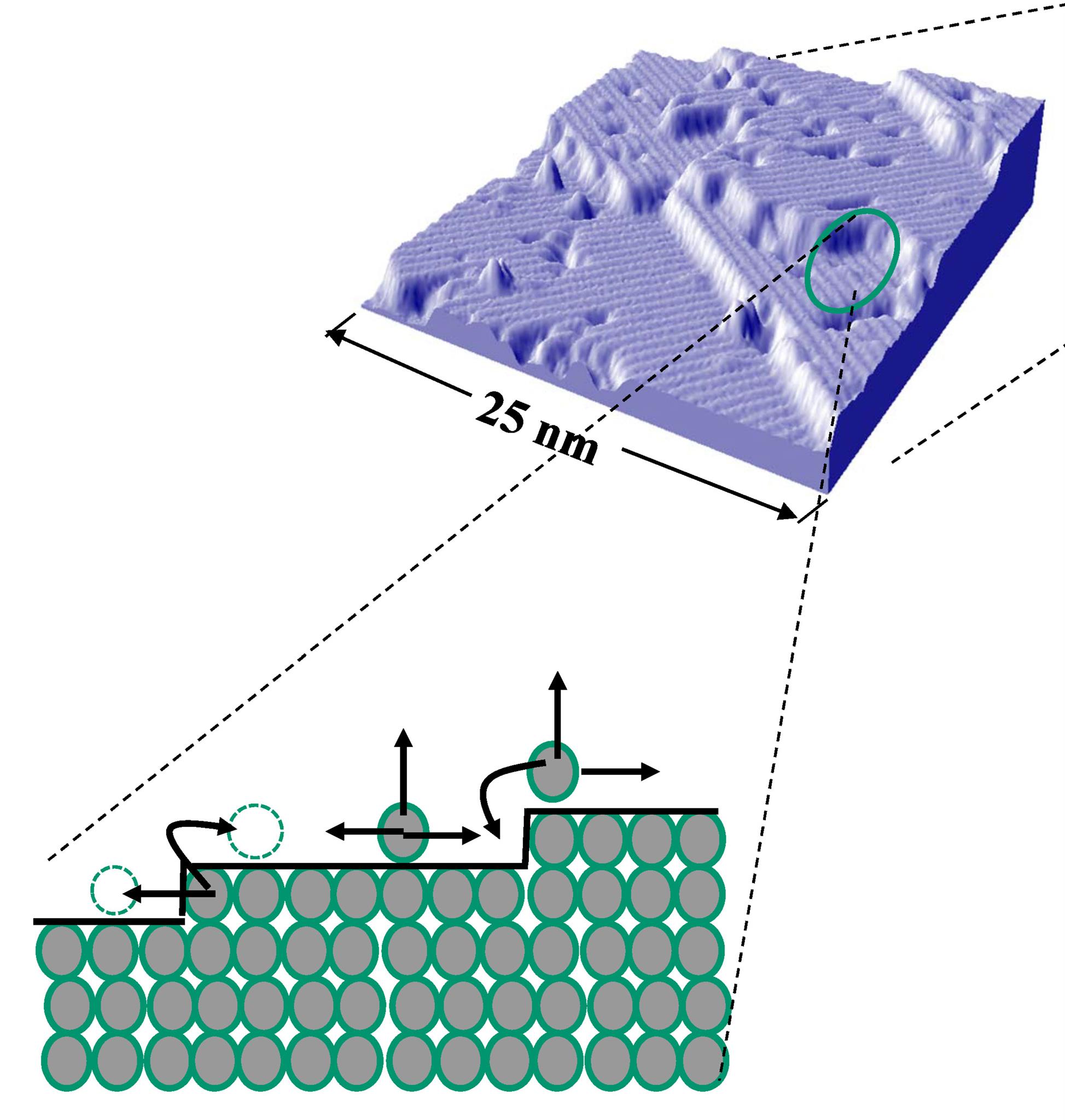
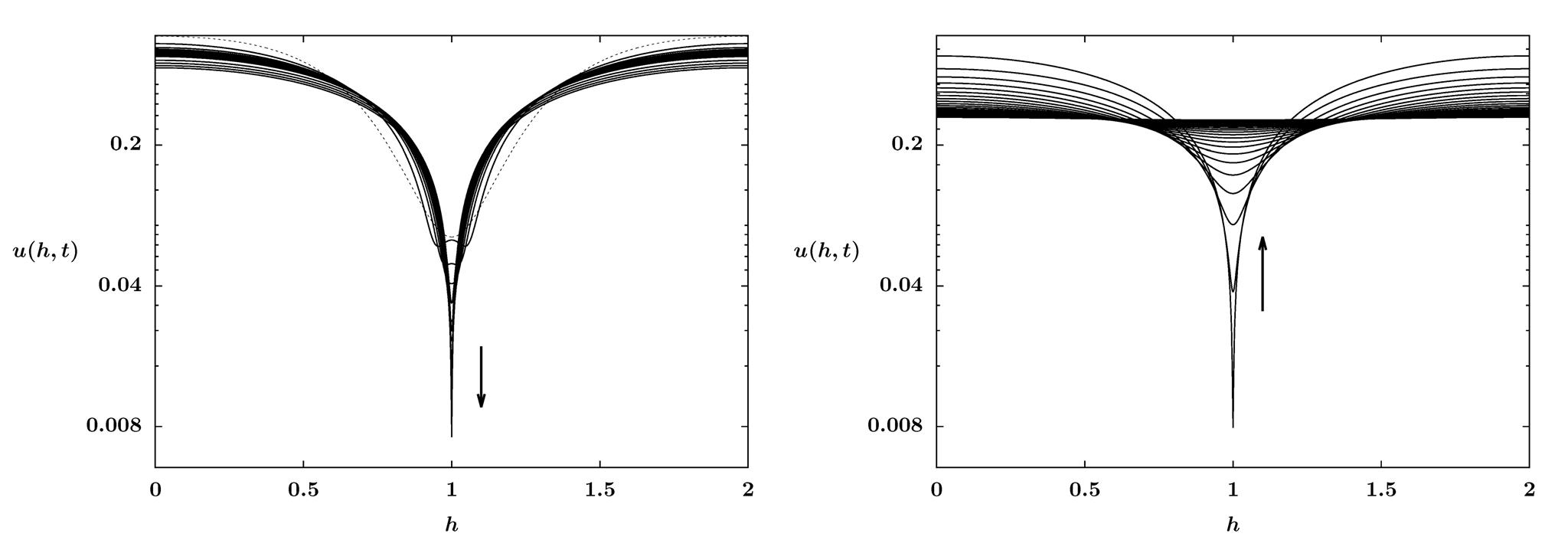
Microscopic surface hopping to BCF step flow
Latent singularity for slope of crystal profile

Related publications:

  1. Gao, Y., J.-G. Liu, and J. Lu. Continuum Limit of a Mesoscopic Model with Elasticity of Step Motion on Vicinal Surfaces. Journal of Nonlinear Science. 27(3): 873–926. (Jun 1, 2017). Full text:
  2. Gao, Y., J.-G. Liu, and J. Lu. Weak solution of a continuum model for vicinal surface in the attachment-detachment-limited regime. Siam Journal on Mathematical Analysis. 49(3): 1705–1731. (Jan 1, 2017). Full text:
  3. Gao, Y., J.-G. Liu, X. Y. Lu, and X. Xu. Maximal monotone operator theory and its applications to thin film equation in epitaxial growth on vicinal surface. Calculus of Variations and Partial Differential Equations. 57(2): 55. (Apr 1, 2018). Full text:
  4. Gao, Y., H. Ji, J.-G. Liu, and T. P. Witelski. A vicinal surface model for epitaxial growth with logarithmic free energy. Discrete and Continuous Dynamical Systems Series B. 23(10): 4433–4453. (Dec 1, 2018). Full text:
  5. Gao, Y., J.-G. Liu, and X. Y. Lu. Gradient flow approach to an exponential thin film equation: Global existence and latent singularity. Esaim Control, Optimisation and Calculus of Variations. 25(49). (Oct 14, 2019). Full text:
  6. Gao, Y.. Global strong solution with BV derivatives to singular solid-on-solid model with exponential nonlinearity. Journal of Differential Equations. 267(7): 4429–4447. (Sep 15, 2019). Full text:
  7. Gao, Y., J.-G. Liu, J. Lu and J. L. Marzuola. Analysis of a continuum theory for broken bond crystal surface models with evaporation and deposition effects. Nonlinearity. 33(8): 3816-3845. (Jun 5, 2020). Full text:
  8. Gao, Y., X. Y. Lu, and C. Wang. Regularity and monotonicity for solutions to a continuum model of epitaxial growth with nonlocal elastic effects. Advances in Calculus of Variations. 000010151520200114. (Apr 16, 2021). Full text:
  9. Gao, Y., A.E. Katsevich, J.-G. Liu, J. Lu, and J.L. Marzuola. Analysis of a fourth order exponential PDE arising from a crystal surface jump process with Metropolis-type transition rates. Pure and Applied Analysis. 3(4): 595-612. (Feb 12, 2022). Full text:

7. Controllability, stabilization for dynamic boundary condition

My research interests also extend to noise control in building materials which derives a system of wave equation coupled with some acoustic boundary conditions. Although there has been some research on system with acoustic boundary condition, there is little result dealing with completely nonlinear oscillatory of boundary materials, especially for uniformly stabilization with only boundary damping.

Related publications:

  1. Gao, Y., J. Liang, and T. J. Xiao. Observability inequality and decay rate for wave equations with nonlinear boundary conditions. Electronic Journal of Differential Equations. 2017(161): 1-12. (Jul 4, 2017). Full text:
  2. Gao, Y., J. Liang, and T. J. Xiao. A new method to obtain uniform decay rates for multidimensional wave equations with nonlinear acoustic boundary conditions. Siam Journal on Control and Optimization. 56(2): 1303–1320. (Jan 1, 2018). Full text:

8. Miscellany

Related publications:

  1. Gao, Y., Y. Gao, and J.-G. Liu. Large Time Behavior, bi-Hamiltonian Structure, and Kinetic Formulation for a Complex Burgers Equation. Quarterly of Applied Mathematics. 79(1): 55-102. (May 21, 2020). Full text:
  2. Gao. Y., and J.-G. Liu. A note on parametric Bayesian inference via gradient flows. Annals of Mathematical Sciences and Applications. 5(2): 261–282. (Oct 13, 2020) Full text: